二分查找

原理

二分查找又称折半查找，使用二分查找有两个要求：

要查找的数列是有序的
数列使用顺序结构存储

二分查找的原理是，对于一个从小到大排序好的数列，首先找到数列中间位置的这个元素，如果此元素大于要查找的数，则证明要找的数在这个元素的前面，查找此元素前一个元素到第一个元素中间的那个元素；如果此元素小于要查找的数，则证明要找的数在这个元素的后面，查找此元素后一个元素到最后一个元素中间的那个元素，后面反复如此，直到找到那个数或者无法再得到中间元素。

举个例子，需要在一个从小到大排序好的数列中查找29。

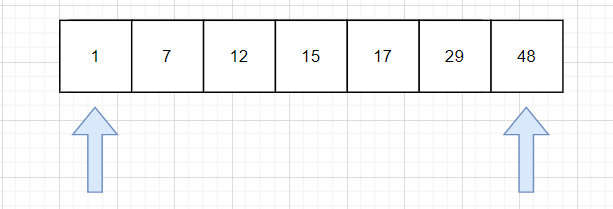
如果是顺序查找，需要6步，即：1 7 12 15 17 29。

而二分查找，我们首先声明两个变量l,r，分别指向第一个元素和最后一个元素，而中间元素可以通过Math.floor((l + r) / 2)来确定。

通过上面的方法，我们找到中间元素是15，它比17小，因此17应该在15的后面，我们把变量l指向17这个元素，r保持不变，再次比较中间元素。

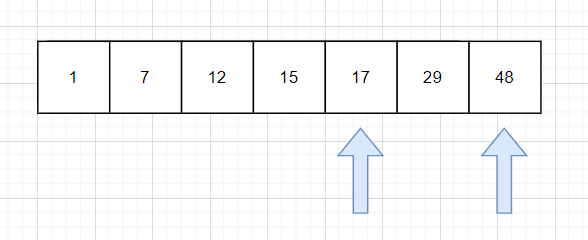
通过Math.floor((l + r) / 2)来确定l和r中间的元素是29，这是我们要查找的数。查找成功。

一般来说二分查找会比顺序查找所花的时间少，尤其是在元素非常多的情况下。

代码实现

JavaScript实现代码

function BinarySearch(arr, n) {
 let l = 0;
 let r = arr.length - 1;
 // 查找结束的条件——无法再找到中间元素
 while (l <= r) {
  const mid = Math.floor((l + r) / 2);
  if (arr[mid] === n) {
   // 查找成功
   return arr[mid];
  } else if (arr[mid] < n) {
   l = mid + 1;
  } else if (arr[mid] > n) {
   r = mid - 1;
  }
 }
 // 没找到
 return false;
}

测试

console.log(BinarySearch([1, 7, 12, 15, 17, 29, 48], 29));
console.log(BinarySearch([1, 7, 12, 15, 17, 29, 48], 17));
console.log(BinarySearch([1, 7, 12, 15, 17, 29, 48], 0));
console.log(BinarySearch([1, 7, 12, 15, 17, 29], 29));
console.log(BinarySearch([1, 7, 12, 15, 17, 29], 15));
// 29
// 17
// false
// 29
// 15

分析

二分查找有个很重要的特点，就是不会查找数列的全部元素，而查找的数据量其实正好符合元素的对数，正常情况下每次查找的元素都在一半一半地减少。所以二分查找的时间复杂度为 O(log2n)。最好的情况只需要查找一遍，最坏的情况和顺序查找一样。

使用二分查找前一定要确保数列是排序好的。

力扣

查找插入位置

题目

给定一个排序的整数数组 nums 和一个整数目标值 target ，请在数组中找到 target ，并返回其下标。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

str

示例 2:

str

示例 3:

str

示例 4:

str

示例 5:

str

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为无重复元素的升序排列数组
-104 <= target <= 104

解题思路

本题给定一个排序的整数数组，要查找target，并且还要求使用时间复杂度为 O(log n) 的算法，很明显是要求我们用二分查找算法。唯一需要考虑的就是题目要求<u>如果目标值不存在于数组中，返回它将会被按顺序插入的位置。</u>

这也很好办，当找不到目标值时，目标值无非就比最后一次查找中间元素nums[mid]小或者大两种情况，**如果是比中间元素小，那么目标值插入到mid的位置，如果目标值比中间元素大，那么目标值插入到mid + 1位置即可。**可以用两组示例验证一下。

nums = [1,3,5,6], target = 4最后一次查找的中间元素是5，目标值4比5小，因此要插入位置为2（即mid）

nums = [1,3,5,6], target = 7最后一次查找的中间元素是6，目标值7比5大，因此要插入位置为4（mid + 1）

代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 $1*/
var searchInsert = function(nums, target) {
    let l = 0
    let r = nums.length - 1;
    let mid;
    while(l <= r){
        mid = Math.floor((l + r) / 2);
        if(nums[mid] === target) {
            return mid;
        }else if(nums[mid] < target){
            l = mid + 1;
        }else if(nums[mid] > target){
            r = mid - 1
        }
    }
    return nums[mid] > target ? mid : mid + 1;
};

山峰数组的顶部

题目

符合下列属性的数组 arr 称为 山峰数组（山脉数组） ：

arr.length >= 3
存在i（0 < i < arr.length - 1）使得：
- arr[0] < arr[1] < ... arr[i-1] < arr[i]
- arr[i] > arr[i+1] > ... > arr[arr.length - 1]

给定由整数组成的山峰数组 arr ，返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i ，即山峰顶部。

示例 1：

str

示例 2：

str

示例 3：

str

示例 4：

str

示例 5：

str

提示：

3 <= arr.length <= 104
0 <= arr[i] <= 106
题目数据保证 arr 是一个山脉数组

**进阶：**很容易想到时间复杂度 O(n) 的解决方案，你可以设计一个 O(log(n)) 的解决方案吗？

解题思路

本题虽然不是排序好的数列，但是遵循从小到大、从大到小的顺序，可以从中间分为从小到大的数列和从大到小的数列，可以尝试使用二分查找，只要找到从小到大数列里最后一个元素即可，这个元素就是山峰顶部。

由题意可得山峰顶部arr[i]必定大于左右两边的元素，因此我们可以用arr[mid]和arr[mid + 1]比较，如果arr[mid] > arr[mid + 1]则arr[mid]可能是山峰顶部（如果此时左边还有更大的数，那么arr[mid]就不是山峰顶部），这时候将右边界r指向mid-1；如果arr[mid] <= arr[mid + 1]，那么山峰顶部应该在arr[mid]右边，将左边界r指向mid + 1，重复以上操作。

代码

/**
 * @param {number[]} arr
 * @return {number}
 $1*/
var peakIndexInMountainArray = function(arr) {
    let l = 0
    let r = arr.length - 1
    let ans = 0;
    while(l <= r){
        let mid = Math.floor((l + r) / 2)
        if(arr[mid] > arr[mid + 1]){
            // ans可能是山峰顶部，而在最后一次arr[mid] > arr[mid + 1]时，mid必定是山峰顶部
            ans = mid; 
            r = mid - 1;
        }else{
            l = mid + 1
        }
    }
    return ans
};